题目链接

leetcode 28 找出字符串中第一个匹配项的下标

如果这个算法有什么不懂的地方，一定要自己画图，一步一步推演，慢慢就会理解

1.KMP算法解决的是一个什么问题

给出两个字符串 ：

主串：aabaabaaf （下文简称为s串）

模式串（也就是匹配串）：aabaaf （下文简称为t串）

我们需要在主串中找到能够和模式串匹配的一段

如果暴力思想的话就是 两层for循环 i和j分别指向s串和t串，一个一个比对，直到j指向t串的最后一位，代表找到了，时间复杂度是O(m*n)，m和n分别表示s和t串的长度。这样当字符串很长或者运气不好（要找的t串在s串的末尾）需要花费的时间是很长的

于是就有三位大神研究出了KMP算法，解决的就是一个问题

2.KMP算法的思想

暴力解法中如果s串和t串已经匹配到最后一位但恰巧最后一位不匹配，那又得重新回头一个一个比较，KMP算法是思路就是能不能不重头匹配，如果不想重头匹配那需要怎么做呢？

观察t串 aabaaf 发现其中是有重复的部分的 例如aa

因此这里需要引入一个数组next[ ] 用来存储一个叫做 最长相等前后缀 的东西

前缀就是a，aa，aab，aaba，aabaa

后缀就是f，af，aaf，baaf，abaaf

注意这里前后缀都不能包括自身串（不然那还叫什么前后呢？）

因此最长相等前后缀很明显其实就是aa，长度为2

于是我们需要将t串中的每一个索引处对应的next数组的值求出来

求出来之后，当我们匹配匹配着发现不匹配的时候，就不用回退到头重新匹配，而是回退到前一个字母的next数组对应的值的下标处，这个点有些绕，可以看图理解：

3.KMP算法的步骤

1.求出next数组

以aabaaf为例

next[0] a 由于前面说过前缀和后缀不能说自身，所以其实是不合规的，因此定义为0

next[1] aa 值为1

next[2] aab 值为0

next[3] aaba 值为1

next[4] aabaa 值为2

next[5] aabaaf 值为0

因此可以得到next数组：[0,1,0,1,2,0]

代码实现： 注意：（i指向的后缀的最后面，j指向的是前缀的最后面）

 //得到next数组
    public int\[\] getNext(int\[\] next,String s){        // 初始化
        int i = 0 ,j = 0;
        next\[0\] = 0;        
        char\[\] a = s.toCharArray();        
        for(i = 1 ;i < s.length();i++){            //前后缀不同的情况
            while(j > 0 && a\[i\] != a\[j\])
                j = next\[j-1\];            //前后缀相同的情况
            if(a\[i\] == a\[j\])
                j++;
            next\[i\] = j;
        }        
        return next;
    }

这里有几个点需要注意一下：

2. 为什么for循环中i从1开始，而非0：如果i从0开始，a[i] == a[j]在一开始会一直成立，导致i和j一起++,程序出错

3. 为什么使用while循环，而非if：if循环只是判断一次，并不能让j回退到需要匹配的地方

4. 为什么j = next[j-1]：next[j-1]表示模式串中前j-1个字符的最长相等前缀和后缀的长度。当a[i] != a[j]时，说明当前的前缀和后缀不匹配，此时需要将j回退到next[j-1]的位置，继续尝试匹配。这个操作相当于利用了已经计算好的next数组信息，避免了从头开始匹配，从而提高了算法的效率。

其实当完成next数组的构建后，就已经约等于解决了，但实际我在做这道题时陷入了匹配的问题

2.开始s串与t串的匹配

下面的haystack就是s串 needle就是t串

首先，考虑两种特殊情况，s串和t串相同，s串的长度小于t串

 // 处理一些特殊情况
        if(needle.isEmpty()) 
            return 0;        
        if(haystack.length() < needle.length())            
        	return -1;

然后，题目给出的是两个字符串，不方便遍历，因此先将其转换为字符数组，并定义一下next数组

 // 定义next数组
        int\[\] next = new int\[needle.length()\];
        getNext(next,needle);        
        // 初始化
        int j = 0 ;        
        char\[\] hay = haystack.toCharArray();        
        char\[\] nee = needle.toCharArray();

最后开始匹配：

 // 开始匹配
        for(int i = 0;i < haystack.length();i++){            
            while(j > 0 && hay\[i\] != nee\[j\]){
                j = next\[j-1\];
            }            
            if(hay\[i\] == nee\[j\]){
                j++;
            }            
            if(j == nee.length){                
                return i-j+1;
            }
        }

在这里，i是一直向前移动的，不会回退，

j指向的是t串，当匹配的上的时候，j++继续匹配，当匹配不上时，j回退的相当于是前j-1个字符的最长相同前后缀的中间值，这样就不用回退到开头了

这里看图理解更清晰：注意图片中next是所有值统一减1的，不影响这个问题

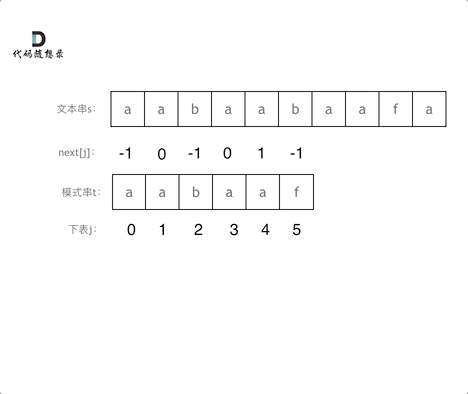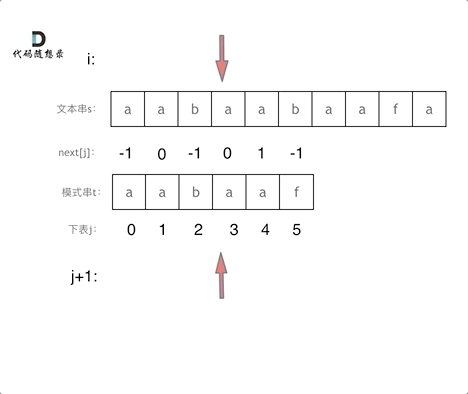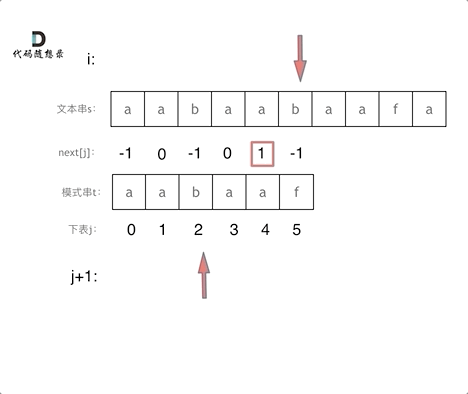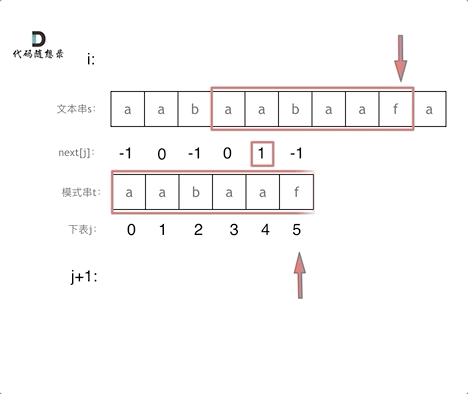
附上完整代码：

class Solution {    
public int strStr(String haystack, String needle) {        // 处理一些特殊情况
        if(needle.isEmpty()) 
            return 0;        
        if(haystack.length() < needle.length())           
           return -1;        
        // 定义next数组
        int\[\] next = new int\[needle.length()\];
        getNext(next,needle);        
        // 初始化
        int j = 0 ;        
        char\[\] hay = haystack.toCharArray();       
        char\[\] nee = needle.toCharArray();        
        // 开始匹配
        for(int i = 0;i < haystack.length();i++){            
        while(j > 0 && hay\[i\] != nee\[j\]){
                j = next\[j-1\];
            }            
            if(hay\[i\] == nee\[j\]){
                j++;
            }           
            if(j == nee.length){                
            return i-j+1;
            }
        }        
        return -1;
    }    //得到next数组
    public int\[\] getNext(int\[\] next,String s){        // 初始化
        int i = 0 ,j = 0;
        next\[0\] = 0;       
        char\[\] a = s.toCharArray();        
        for(i = 1 ;i < s.length();i++){            
        	while(j > 0 && a\[i\] != a\[j\])
                j = next\[j-1\];            
            if(a\[i\] == a\[j\])
                j++;
            next\[i\] = j;
        }        
        return next;
    }
}